-
Compteur de contenus
426 -
Inscription
-
Dernière visite
-
Trophée
5
Frédéric NAUD last won the day on 13 avril
Frédéric NAUD had the most liked content!
À propos de Frédéric NAUD
- Date de naissance 10/09/1974
Informations Personnelles
-
Localisation
Dienville (10) / FRANCE
-
Profession / Occupation
Professeur de mathématiques
Informations Magiques
-
Club(s) / Association(s) / Cercle(s)...
Académie Magique de Champagne (Troyes)
-
Connaissances Utiles pour Notre Art :
Musique (Guitare), mathématiques, dessin
Visiteurs récents du profil
3396 visualisations du profil
Frédéric NAUD's Achievements
-
L'étape 6 est terrible (même sans la partie en italique) !
-

David COPPERFIELD accusé de violences sexuelles
Frédéric NAUD a répondu à un sujet de Philippe SACCOMANO dans Forum Général
Je pense qu'il ne faut pas dire les choses comme ça... Je préfère : "Actuellement, on ne prend aucune décision, on ne commet aucun acte qu'on prendrait ou commettrait s'il était coupable". Mais on ne dit pas qu'il est innocent ! On ne dit rien, c'est tout ! Même chose... Le fait d'être innocent ou coupable d'un acte passé n'a ensuite rien à voir avec la temporalité ("actuellement", "en attendant"...). C'est la considération d'un point de vue officiel (public, judiciaire) qui elle dépend du temps et doit être postérieure à la décision de justice. Après chacun ses réflexions et son ressenti personnels face à une affaire. Il ne faut pas juger sans savoir, mais dans les deux sens. On entend par exemple des représentants de l'état "apporter leur soutien" à des gens accusés qui appartiennent à leur sphère (politique, sociale, culturelle...), sous prétexte de la présomption d'innocence, alors qu'ils n'ont à mon avis pas plus de légitimité que ce que tu appelles la vox populi. On peut éventuellement témoigner sa confiance envers quelqu'un qui est accusé si on le pense innocent, mais il s'agit alors d'un engagement personnel ou partisan. Un personnage public devra alors faire profil bas s'il s'est trompé, et c'est carrément inacceptable venant d'un représentant de l'état. Beaucoup s'élèvent aussi contre une soi-disant vindicte populaire parce qu'ils sentent que certaines choses sont en train de changer, et qu'au mieux elles remettent leur façon de voir les choses en question, au pire elles pointent certaines de leurs habitudes répréhensibles qu'ils s'avouent ou pas à eux-mêmes. -

David COPPERFIELD accusé de violences sexuelles
Frédéric NAUD a répondu à un sujet de Philippe SACCOMANO dans Forum Général
Mickaël, c'est toi qui nous met une citation disant que la justice "considère" comme innocent quelqu'un qui dont la culpabilité n'a pas été prouvée. Le terme "considéré" n'a pas été choisi à la légère : il veut dire que même si on ne sait pas ce qu'il en est, on fait comme si la personne était innocente. Malheureusement non, on condamne parfois des innocents... -

David COPPERFIELD accusé de violences sexuelles
Frédéric NAUD a répondu à un sujet de Philippe SACCOMANO dans Forum Général
Il y a une grosse différence entre être factuellement innocent et être considéré comme innocent d'un point de vue judiciaire... -
Tu as tendance à commettre des impairs en écrivant des "impaires"...
-
D'où l'expression "non binaire".
-

Ambitious all the Way de John CAREY
Frédéric NAUD a répondu à un sujet de Nicholas RYL dans Forum Général
J'ai pensé au début à un sdc couvert par la séparation des deux paquets (le classique "grand mouvement qui cache le petit") mais si c'est ça, effectivement la qualité de la vidéo, ainsi que (et surtout !) la qualité des manips (il s'agit bien de Carey himself non ?) aide à masquer le move. -

Ambitious all the Way de John CAREY
Frédéric NAUD a répondu à un sujet de Nicholas RYL dans Forum Général
J'aime beaucoup. La phase à partir de 1:23 me laisse pantois... C'est vraiment la même carte ? -
Pour Al Baker. Pour la demoiselle, c'est pas sûr...
-
Peut-être pas... Au moins un des spectateurs sur scène oui par contre... J'attends le jour où un spectateur utilisé comme ça va ramener sa fraise lors d'un spectacle en direct. Remarque elle a pris ses précautions : pas de réactions m'ssieurs dames ! Ces techniques reposent beaucoup sur la sensation qu'a le spectateur de participer au tour, d'être un partenaire du magicien, sur la fierté d'être dans la confidence. Ce qui me surprend encore, c'est que, étant donné que les complices instantanés doivent quand même parler de ce qui s'est réellement passé, au moins à leurs proches, et que ce genre de technique est quand même assez fréquente actuellement, l'info ne se répande pas plus vite. Le public des spectacles de magie n'est peut-être que majoritairement un public occasionnel chez qui les infos sur les "trucs" tombent vite aux oubliettes, ou alors de véritables amateurs qui s'imposeront plus ou moins de respecter la loi du secret.
-

Possibilités de votre Jeu de 52 Cartes
Frédéric NAUD a répondu à un sujet de Theo VITTE dans Forum Général
Tout ça est ok sauf que dans l'histoire, la fonction f n'est pas une probabilité, non ? C'est juste une bijection de IR sur ]0;1[ (et je pense que n'importe laquelle convient dans la mesure où elle est strictement croissante). La variable s quand elle suit la loi uniforme sur [0;1]. Voici la preuve que tu me demandais : Jeu Frédéric Hô bis.pdf Cette stratégie est sympa. Par contre la proba dépend des nombres inscrits... Pour se rendre compte de l'efficacité de la stratégie, il faudrait travailler sur f(G) - f(P) et donc sur le choix de la fonction f. Effectivement, la proba de gagner en adoptant la stratégie : "si le nombre inscrit sur le papier choisi est supérieur ou égal à 1/2, on parie que c'est lui le plus grand, sinon on parie sur un autre au hasard" doit donner une probabilité de gagner supérieure à 1/2. Autre chose sur ton jeu d'origine : voici une version un peu plus générale de ce que j'ai (je pense) démontré : Le joueur 1 inscrit au hasard sur un papier un nombre réel x de l'intervalle ]-A;A[ (où A est un réel strictement positif), puis sur un autre papier un nombre réel y différent de x, lui aussi dans ]-A;A[. Le joueur 2 choisit un papier. La stratégie : "si le nombre inscrit sur le papier choisi est supérieur ou égal à 0, on parie que c'est lui le plus grand, sinon on parie sur l'autre" donne encore (avec un calcul un peu plus compliqué mais similaire à celui que j'ai posté précédemment) une probabilité de gagner de 3/4, quelque soit la valeur de A. Faire tendre A vers l'infini est possible mais ne nous affranchit pas de choisir x et y dans ]-A;A[ dès le début, et de conditionner les probabilités calculées au choix de A. -

Possibilités de votre Jeu de 52 Cartes
Frédéric NAUD a répondu à un sujet de Theo VITTE dans Forum Général
Je pense avoir prouvé ce qui suit : Avec ce processus : le joueur 1 marque au hasard un nombre x de [0;1] sur un papier puis un nombre y de [0;1] différent de x sur un autre papier, le joueur 2 choisit au hasard un des deux papiers, le joueur 2 a une chance sur 2 d'avoir le plus grand des deux nombres x et y s'il garde le nombre du papier qu'il a choisi (stratégie 1), il a 3 chances sur 4 d'avoir le plus grand des deux nombres x et y s'il opte pour la stratégie 2 : garder le nombre du papier qu'il a choisi si celui-ci est supérieur ou égal à 1/2, prendre le nombre du papier qu'il n'a pas choisi sinon. Preuve (j'espère) ici : jeu Frédéric Hô.pdf -

Possibilités de votre Jeu de 52 Cartes
Frédéric NAUD a répondu à un sujet de Theo VITTE dans Forum Général
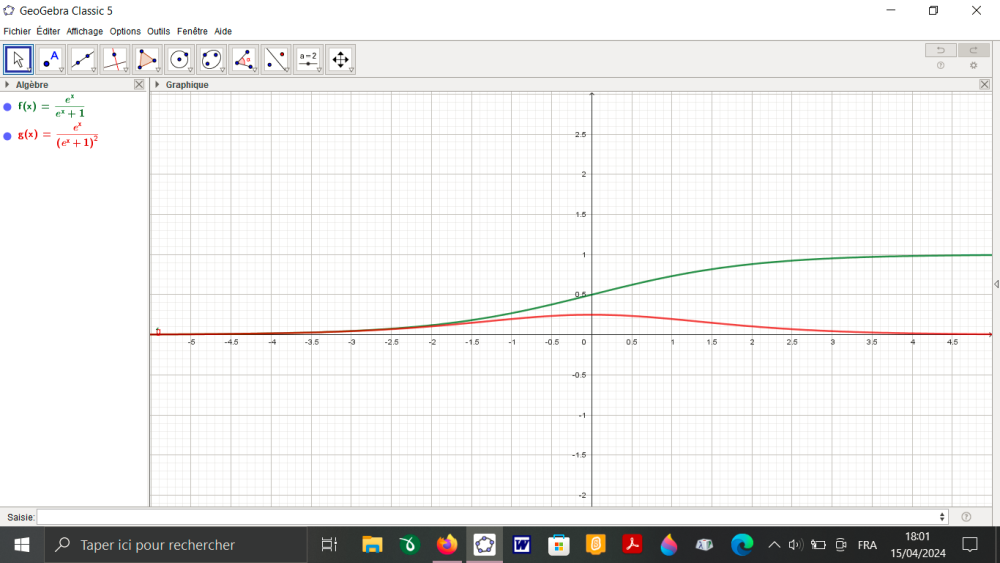
Ta fonction f peut définir une fonction de répartition pour une loi à densité. Ta fonction correspond à la courbe verte ci-dessus et la densité à la courbe rouge. L'intégrale de -infini à + infini est bien égale à 1. Je pense à une loi uniforme car pour le problème que je me suis posé (pas encore celui de ton jeu) si on considère la probabilité qu'un réel x différent de 0 choisi au hasard soit supérieur à 0, le nombre choisi doit, avoir autant de chances d'être par exemple dans l'intervalle [1;2] que dans l'intervalle [2;3] ou n'importe quel autre intervalle fermé de longueur 1, dans la mesure où il ne contient pas 0. On doit avoir P(1<x<2) = P(2<x<3). -

Possibilités de votre Jeu de 52 Cartes
Frédéric NAUD a répondu à un sujet de Theo VITTE dans Forum Général
Remarque moi aussi, je multiplie les messages...
- Pas de pub non magique pour les membres du Cercle VM. Clique ici pour en savoir plus !
-
Qui est en ligne (en orange les membres du Cercle VM) - 1 membre, 0 anonyme, 98 invités Afficher la liste